The reference of the below article is here.
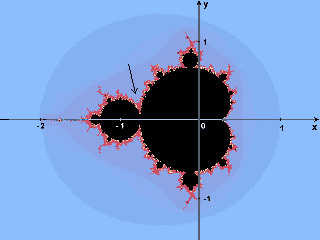
In 1991 David Bolle tried to verify if the narrowing we can see at (-0.75,0) was actually infinitely thin. That is to say that that however wide a non-zero width vertical line would be passing through that point it would meet the fractal set before the x-axis.
And D Bolle then had the idea of using the
point c=(-0.75,X) for the quadratic iteration and to make X tend to 0. And
there, what was his surprise when he counted the number of iterations before
which the series diverged and by discovering the following table:
| X | iterations |
|---|---|
| 1.0 | 3 |
| 0.1 | 33 |
| 0.01 | 315 |
| 0.001 | 3143 |
| 0.0001 | 31417 |
| 0.00001 | 314160 |
| 0.000001 | 3141593 |
| 0.0000001 | 31415928 |
Yes, it was Pi that was appearing magnificientely ! As he could not manage
to prove this he posted it in 1992 on the sci.maths newsgroup. Gerald Edgar
from a university of Ohio answered it on 27 march 1992 by bringing an intuitive
explanation of this result. This has been put lower down in the "Trial"
section.
After this David Bolle approached the problem
with another point c=(0.25+X,0) which were those of the... well... butt part of
the set on the right.
Once again, same surprise, this time it is X1/2*n which tends to Pi.
| X | iterations |
|---|---|
| 1.0 | 2 |
| 0.1 | 8 |
| 0.01 | 30 |
| 0.001 | 97 |
| 0.0001 | 312 |
| 0.00001 | 991 |
| 0.000001 | 3140 |
| 0.0000001 | 9933 |
| 0.00000001 | 31414 |
| 0.000000001 | 99344 |
| 0.0000000001 | 314157 |
In our visualization example, use c=(0.25+X, 0), X=1E-14